Modellazione parametrica: definizione, funzionamento e applicazioni
La modellazione parametrica rappresenta un approccio avanzato nella progettazione assistita da computer che permette di creare e manipolare modelli 3D intelligenti attraverso l’uso di parametri e relazioni definite. A differenza della modellazione tradizionale, dove le geometrie hanno dimensioni fisse, nella modellazione parametrica ogni elemento è definito da variabili modificabili che controllano dimensioni, posizioni e proprietà.
SHIN Software è specializzata in configuratori 3D di prodotti
Questo metodo di progettazione si distingue per la sua natura dinamica: quando un parametro viene modificato, tutti gli elementi correlati si aggiornano automaticamente, mantenendo intatte le relazioni stabilite. Grazie alla modellazione parametrica, i progettisti possono modificare facilmente i loro modelli in base a parametri variabili, esplorando rapidamente diverse soluzioni progettuali senza dover ricostruire il modello da zero.
Il concetto fondamentale alla base di questo approccio è la preservazione dell’intento progettuale: il modello “comprende” come deve comportarsi quando vengono apportate modifiche, garantendo che il design mantenga la sua coerenza e funzionalità.
Come funziona la modellazione parametrica
Nella modellazione parametrica, i parametri sono le variabili che definiscono il comportamento del modello. Questi possono includere dimensioni (lunghezza, larghezza, altezza), proprietà dei materiali, relazioni geometriche o persino indicatori di prestazione. Il design parametrico permette di creare forme complesse attraverso algoritmi e relazioni matematiche, consentendo ai progettisti di controllare con precisione ogni aspetto del modello.
Nella modellazione parametrica, i parametri sono le variabili che definiscono il comportamento del modello. Questi possono includere dimensioni (lunghezza, larghezza, altezza), proprietà dei materiali, relazioni geometriche o persino indicatori di prestazione. Il design parametrico permette di creare forme complesse attraverso algoritmi e relazioni matematiche, consentendo ai progettisti di controllare con precisione ogni aspetto del modello.
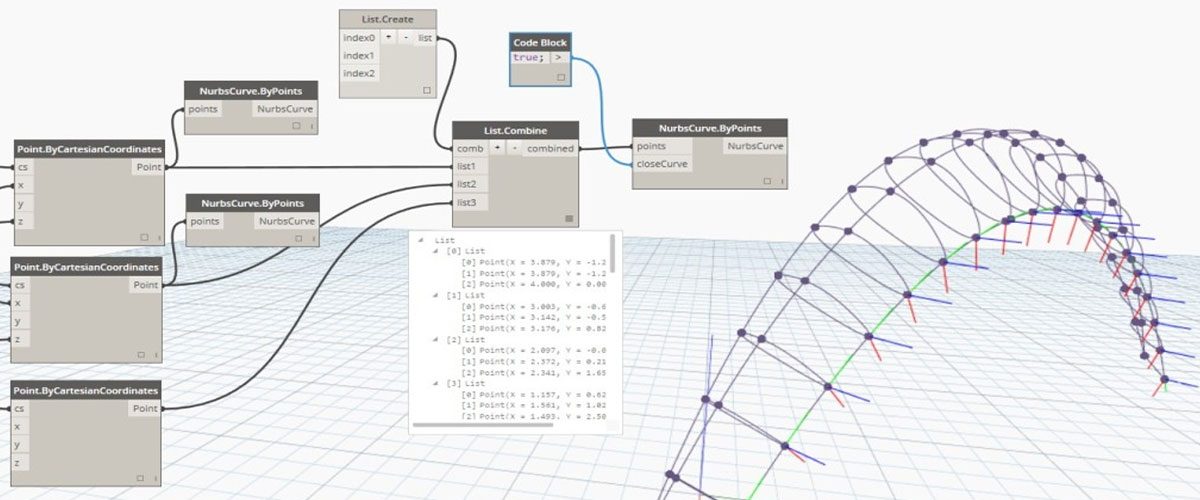
Relazioni e vincoli: la parametrizzazione geometrica
Il cuore della modellazione parametrica risiede nelle relazioni e nei vincoli che collegano i diversi elementi del modello. La parametrizzazione geometrica consente di definire forme attraverso parametri modificabili anziché dimensioni fisse. Questi vincoli possono essere di vario tipo:
- Vincoli geometrici (parallelismo, perpendicolarità, tangenza)
- Vincoli dimensionali (distanze, angoli, raggi)
- Vincoli di simmetria o pattern
- Vincoli di posizione relativa
Quando un elemento viene modificato, tutti gli elementi correlati si adattano automaticamente per rispettare i vincoli stabiliti, garantendo la coerenza del modello.
Il concetto di “storia di costruzione”
Un aspetto fondamentale della modellazione parametrica è la “storia di costruzione” (tree history), che registra la sequenza di operazioni utilizzate per creare il modello. Questa cronologia permette di tornare indietro e modificare qualsiasi passaggio della progettazione, con il sistema che ricalcola automaticamente tutti i passaggi successivi.
Con la modellazione 3D parametrica, ogni elemento del modello mantiene relazioni intelligenti con gli altri componenti, creando un sistema interconnesso che preserva l’intento progettuale anche durante modifiche sostanziali.
Applicazioni della modellazione parametrica
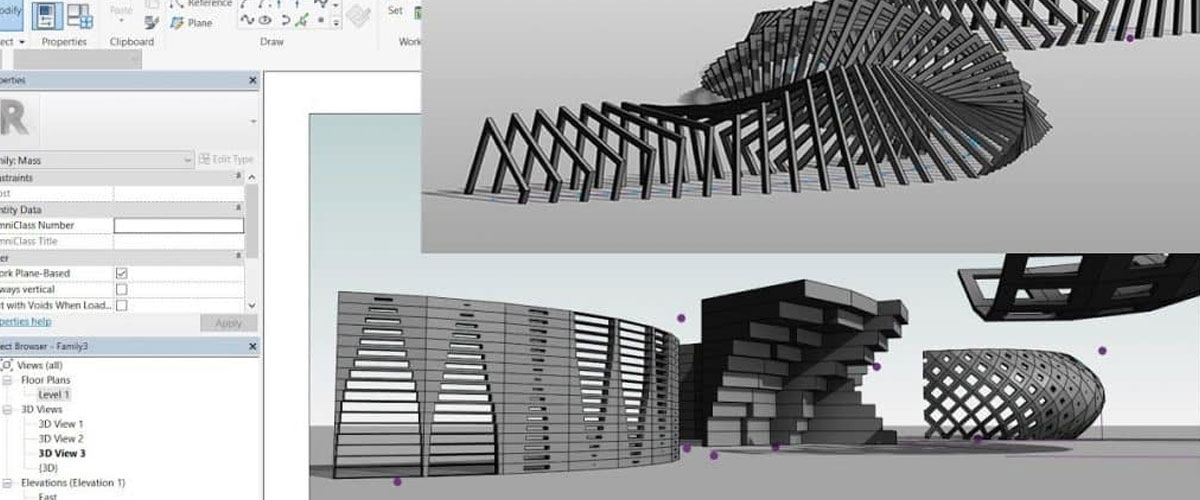
Modellazione parametrica nell’architettura
L’adozione della modellazione parametrica sta rivoluzionando diversi settori industriali, a partire dall’architettura. Nell’architettura contemporanea, il design parametrico ha aperto nuove possibilità estetiche e funzionali, permettendo la creazione di forme complesse e organiche che sarebbero state difficili da realizzare con metodi tradizionali.
Il BIM parametrico integra informazioni dettagliate sui materiali e le prestazioni degli elementi costruttivi, consentendo analisi strutturali, energetiche e di costo in tempo reale. L’adozione del BIM parametrico migliora significativamente la collaborazione tra i diversi professionisti coinvolti in un progetto, dalla progettazione alla costruzione e gestione dell’edificio.
Modellazione parametrica nel design industriale
Nel design industriale, la modellazione parametrica consente di creare famiglie di prodotti che condividono caratteristiche comuni ma si adattano a requisiti specifici. Questo approccio è particolarmente utile per:
- Personalizzazione di massa di prodotti
- Ottimizzazione di componenti per prestazioni specifiche
- Creazione di varianti di prodotto mantenendo l’identità del brand
- Prototipazione rapida e iterativa
Attraverso la progettazione parametrica, è possibile esplorare rapidamente diverse varianti di design, accelerando il processo di sviluppo del prodotto e riducendo i costi di prototipazione.
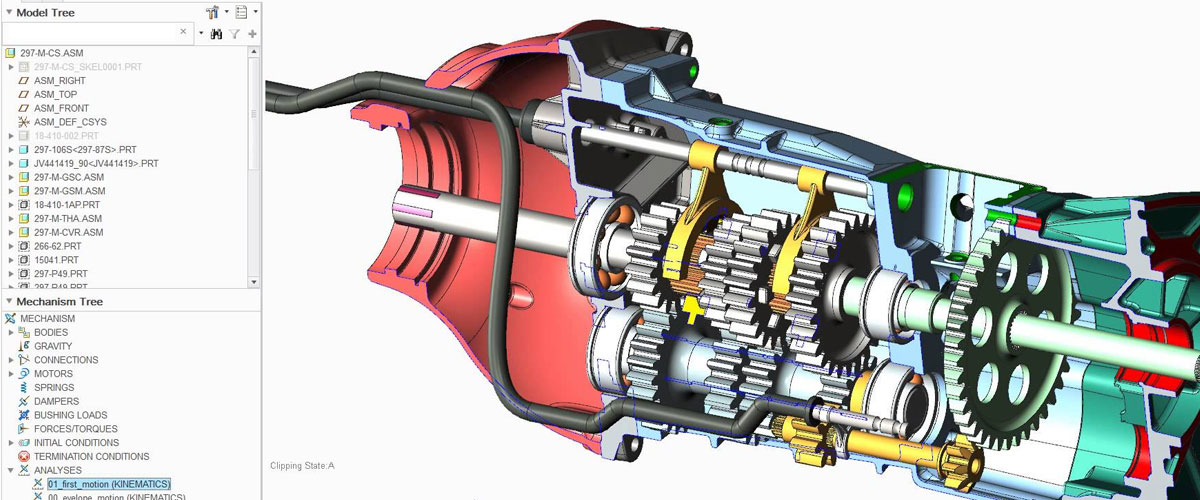
Modellazione parametrica nell’ingegneria meccanica
Nell’ingegneria meccanica, la modellazione parametrica offre strumenti potenti per la progettazione di componenti e sistemi complessi. Gli ingegneri possono definire relazioni funzionali tra le parti, garantendo che i componenti si adattino correttamente anche quando le specifiche cambiano.
Questo approccio è fondamentale per:
- Progettazione di sistemi meccanici complessi
- Ottimizzazione topologica di componenti
- Analisi strutturali e simulazioni di prestazioni
- Gestione di assemblaggi con numerosi componenti interdipendenti
Vantaggi della modellazione parametrica
Flessibilità e modificabilità del design
Uno dei principali vantaggi della modellazione parametrica è la flessibilità che offre ai progettisti. Le modifiche possono essere apportate in qualsiasi fase del processo di progettazione, con il sistema che aggiorna automaticamente l’intero modello. Questo permette di:
- Esplorare rapidamente alternative di design
- Rispondere prontamente a cambiamenti nei requisiti
- Adattare i progetti a diverse condizioni o vincoli
- Iterare più velocemente verso soluzioni ottimali
Ottimizzazione del tempo di progettazione
La modellazione parametrica riduce drasticamente i tempi di progettazione, soprattutto quando si tratta di apportare modifiche o creare varianti di un design esistente. Invece di ricostruire il modello da zero, i progettisti possono semplicemente modificare i parametri rilevanti e lasciare che il sistema ricalcoli automaticamente la geometria.
Questo approccio è particolarmente vantaggioso per progetti complessi o per situazioni in cui i requisiti cambiano frequentemente durante il processo di sviluppo.
Precisione e controllo dei dettagli
La progettazione parametrica si basa sulla definizione di relazioni tra gli elementi piuttosto che sulla loro geometria fissa, garantendo un livello di precisione e controllo superiore rispetto ai metodi tradizionali. I progettisti possono definire con esattezza come ogni elemento deve comportarsi in relazione agli altri, assicurando che il design mantenga la sua integrità anche durante modifiche sostanziali.
Termini correlati
- Design generativo: metodologia che utilizza algoritmi per esplorare automaticamente variazioni di design basate su parametri e vincoli definiti.
- Digital Twin: rappresentazione digitale parametrica di un oggetto o sistema fisico, utilizzata per simulazioni e analisi.
- BIM (Building Information Modeling): processo che integra la modellazione parametrica con informazioni dettagliate su materiali, costi e prestazioni nell’ambito dell’architettura e delle costruzioni.
- Prototipazione parametrica: processo di creazione rapida di prototipi fisici basati su modelli parametrici, spesso utilizzando tecnologie di stampa 3D o fabbricazione digitale.
- Ottimizzazione topologica: tecnica che utilizza algoritmi parametrici per ottimizzare la distribuzione del materiale in un componente in base a vincoli strutturali e di prestazione.